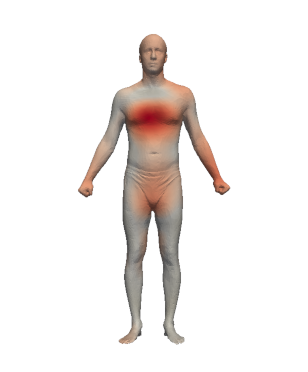
At the end of the computation (a few hours with a high performance graphic cards), the output contains a mean shape and the deformations from the mean shape to each specimen.
The result folder can be downloaded here.
Example of deformations (mouse over to see animation):
One can compute a principal component analysis (PCA) to visualise the results in 2 or 3 dimensions with RToolsForDeformetrica:
To install RToolsForDeformetrica with R :
download.file(
"https://gitlab.com/jeandumoncel/tools-for-deformetrica/-/raw/master/src/R_script/RToolsForDeformetrica/RToolsForDeformetrica_0.1.tar.gz",
"RToolsForDeformetrica_0.1.tar.gz"
)
install.packages("RToolsForDeformetrica_0.1.tar.gz", repos = NULL, type = "source")
To plot the PCA:
library(RToolsForDeformetrica)
###############
NumberOfSubject = 3045# number of subjects (pooled)
group = as.factor(c(rep(1,times=1531),rep(2,times=1514)))
KernelWidth = 0.1# kernel width of the deformation kernel
#MomentaPathname = file.choose()
MomentaPathname = '../output/DeterministicAtlas__EstimatedParameters__Momenta.txt'
# ControlPointsPathname = file.choose()
ControlPointsPathname = '../output/DeterministicAtlas__EstimatedParameters__ControlPoints.txt'
##############
Momenta = import_momenta(MomentaPathname, NumberOfSubject)
ControlPoints = import_control_points(ControlPointsPathname)
velocities = compute_velocities(Momenta$momenta, ControlPoints, KernelWidth)
ColumnMean = colMeans(velocities$V)
velocitiesC = velocities$V-matrix(rep(ColumnMean,nrow(velocities$V)),nrow=nrow(velocities$V),ncol=ncol(velocities$V),byrow=TRUE)
gp = prcomp(velocitiesC,scale = FALSE,center=FALSE)
ev <- (1-1/dim(gp$x)[1])*(gp$sdev^2)
variance = round(ev/sum(ev)*100, digits=2)
plot(gp$x[,1],gp$x[,2],asp=1,pch=1,col=group, xlab="", ylab="")
convex_hull(gp$x, group)
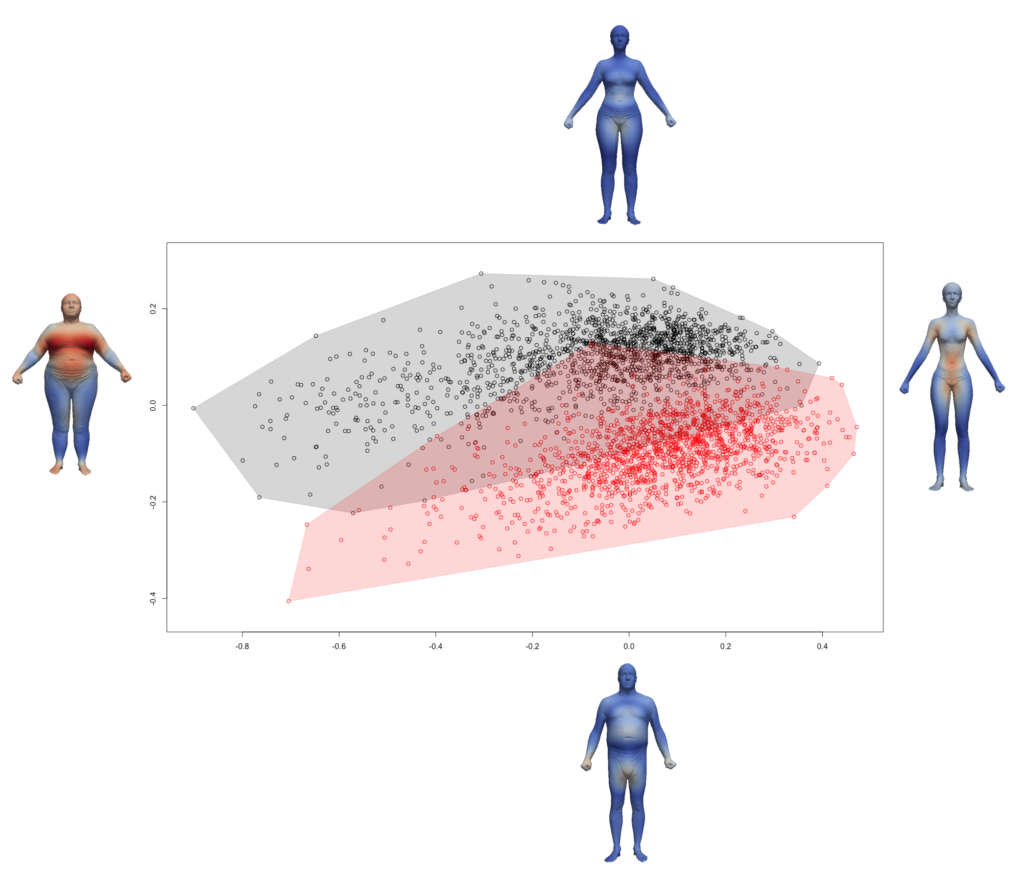
Ce qui permet d'obtenir le graphique suivant (cf le dossier de résultats pour les conformations extrêmes) :
One get this graphic (cf resultats folder for the extrem conformations):
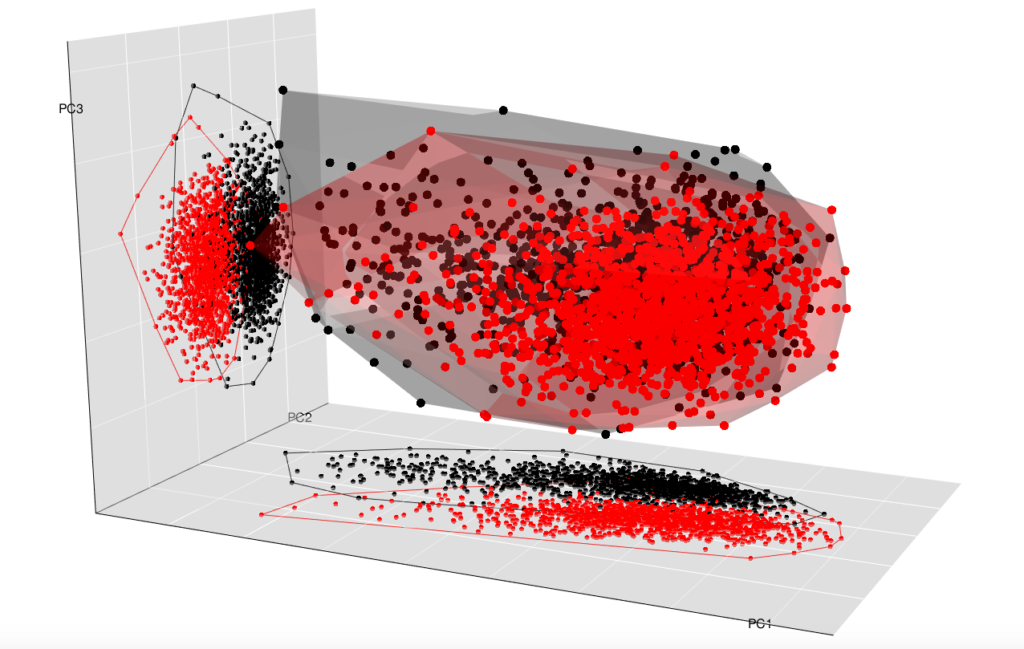
The same analysis with 3 components:
my3dplot(gp$x,group,xy = T, yz = T, xz = F)