Une fois les calculs effectués (après quelques heures avec une carte graphique performante), nous obtenons une forme moyenne ainsi que les déformations de la forme moyenne vers chaque spécimen.
Le dossier contenant une partie des résultats ainsi que les analyses peut être téléchargé ici.
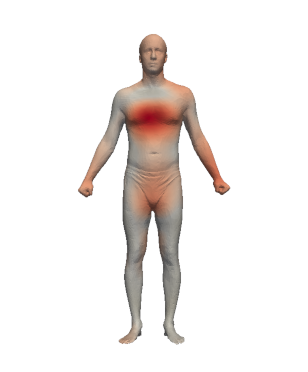
Exemple de déformations obtenues (passez la souris sur l’image pour jouer l’animation) :
Il est alors possible d’effectuer une analyse en composante principale (ACP) pour visualiser les résultats en 2 ou 3 dimensions en utilisant RToolsForDeformetrica :
Pour installer RToolsForDeformetrica dans R :
download.file(
"https://gitlab.com/jeandumoncel/tools-for-deformetrica/-/raw/master/src/R_script/RToolsForDeformetrica/RToolsForDeformetrica_0.1.tar.gz",
"RToolsForDeformetrica_0.1.tar.gz"
)
install.packages("RToolsForDeformetrica_0.1.tar.gz", repos = NULL, type = "source")
Pour générer le graphique :
library(RToolsForDeformetrica)
###############
NumberOfSubject = 3045# number of subjects (pooled)
group = as.factor(c(rep(1,times=1531),rep(2,times=1514)))
KernelWidth = 0.1# kernel width of the deformation kernel
#MomentaPathname = file.choose()
MomentaPathname = '../output/DeterministicAtlas__EstimatedParameters__Momenta.txt'
# ControlPointsPathname = file.choose()
ControlPointsPathname = '../output/DeterministicAtlas__EstimatedParameters__ControlPoints.txt'
##############
Momenta = import_momenta(MomentaPathname, NumberOfSubject)
ControlPoints = import_control_points(ControlPointsPathname)
velocities = compute_velocities(Momenta$momenta, ControlPoints, KernelWidth)
ColumnMean = colMeans(velocities$V)
velocitiesC = velocities$V-matrix(rep(ColumnMean,nrow(velocities$V)),nrow=nrow(velocities$V),ncol=ncol(velocities$V),byrow=TRUE)
gp = prcomp(velocitiesC,scale = FALSE,center=FALSE)
ev <- (1-1/dim(gp$x)[1])*(gp$sdev^2)
variance = round(ev/sum(ev)*100, digits=2)
plot(gp$x[,1],gp$x[,2],asp=1,pch=1,col=group, xlab="", ylab="")
convex_hull(gp$x, group)
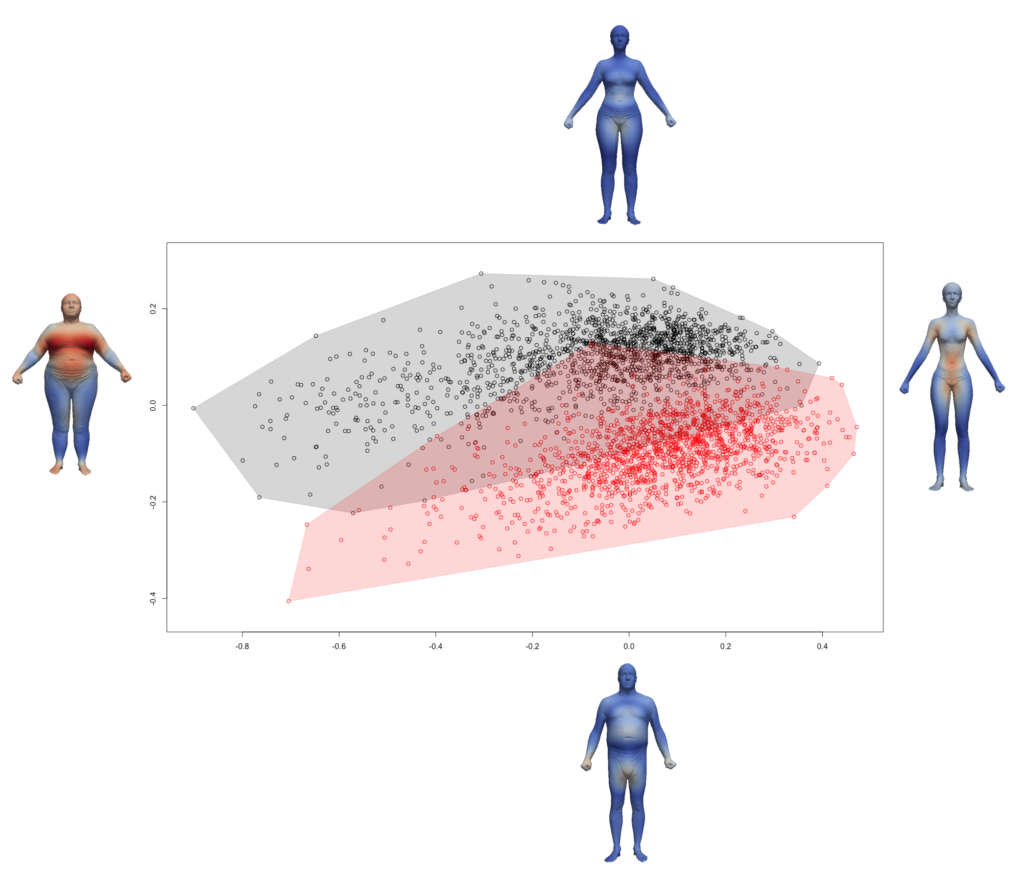
Ce qui permet d'obtenir le graphique suivant (cf le dossier de résultats pour les conformations extrêmes) :
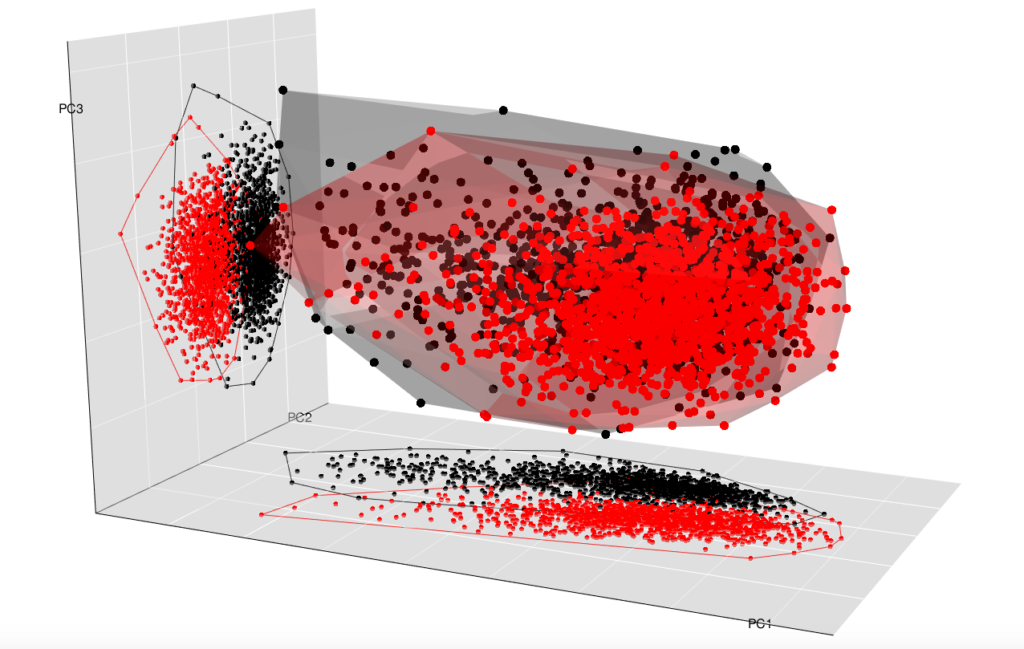
La même analyse avec les 3 premières composantes :
my3dplot(gp$x,group,xy = T, yz = T, xz = F)